La Escuela del Programador

Las expresiones lambda, si bien son algo nuevo en Visual Basic o C#, se basan en un concepto matemático de ya casi 80 años: El cálculo lambda. El cálculo lambda, es un formalismo matemático que fue introducido por Alonzo Church en el año 1934. Para entender este sencillo concepto matemático tomemos dos funciones:

Por un lado, la función identidad f(x) = x, que toma un único argumento, x, e inmediatamente devuelve x.

Por otro lado, la función suma f(x,y) = x + y, que toma dos argumentos, x e y, y devuelve la suma de ambos: x + y.

Usando estas dos funciones como ejemplo, es posible hacer algunas observaciones útiles acerca de varias ideas fundamentales del cálculo lambda: La primera observación es que las funciones no necesitan ser explícitamente nombradas. Esto es, la función f(x,y) = x + y puede ser reescrita como una función anónima: (x,y) → x + y (que se lee: «el par de x e y se mapea a x + y»). Del mismo modo, f(x) = x puede ser reescrita de forma anónima como x → x, que se lee: «el argumento x se mapea a sí mismo».

La segunda observación es que el nombre que se asigne a los argumentos de la función es generalmente irrelevante. Esto es, x → x e y → y expresan la misma función: la función identidad. Del mismo modo, x,y → x + y y u,v → u + v expresan la misma función: la función suma de dos números.

Una tercera observación es que toda función que requiere dos argumentos, como por ejemplo la función suma, puede ser reescrita como una función que acepta un único argumento, pero que devuelve otra función, la cual a su vez acepta un único argumento. Por ejemplo, x,y → x + y puede ser reescrita como x → (y → x + y). Esta transformación se conoce como currificación, y puede generalizarse para funciones que aceptan cualquier número de argumentos. Esta puede parecer oscuro, pero se entiende mejor mediante un ejemplo. Considérese la función suma no currificada: x,y → x + y Al tomar a los números 4 y 5 como argumentos, se obtiene: 4 + 5 Lo cual es igual a 9. Considérese ahora la versión currificada de la función: x → (y → x + y) Si se toma al número 4 como argumento x, se obtiene la función: y → 4 + y Y tomando luego al número 5 como argumento y, se obtiene: 4 + 5 Lo cual es igual a 9. De modo que la versión currificada devuelve el mismo resultado que la versión no currificada. En el cálculo lambda, todas las expresiones representan funciones anónimas de un sólo argumento.

En el cálculo lambda, las funciones están definidas por expresiones lambda, que dicen qué se hace con su argumento. Por ejemplo, la función "sumar 2": f(x) = x + 2 se expresa en cálculo lambda así: λ x. x + 2. El valor de f(3) sería escrito como (λ x. x + 2) 3

Esto ha sido llevado a la programación .NET y a partir de Visual Studio 2008, tanto C#, como VB, admiten funciones anónimas utilizando expresiones lambda.

Claro que la sintáxis de C# se acerca mas a la original matemática ya que en C# podemos definir el siguiente código antiguo:

function int Suma(int x, int y)
{
   return x + y;
}

de la siguiente manera:

(x, y) => x + y;

Mientras que la función equivalente en Visual Basic:

Function Suma (x As Integer, y As Integer) As Integer
   return x + y;
End Function

debe ser escrita usando expresiones lambda de la siguiente manera (note que Visual Basic, necesita más código):

Function(x, y) x + y

Vemos que la expresión lambda en C# se acerca mas a la representación matemática, si bien no hay ninguna diferencia desde el punto de vista de que ambos lenguajes admiten expresiones lambda.

Otros ejemplos de expresiones lambda

1. Veamos por ejemplo como escribir en ambos lenguajes una función que no toma argumentos y devuelve una cadena especifica: En VB:

  Function Saluda() as String
    return " Hola mundo!"
  End Sub

En C#:

 function String Saluda()
 {
    return " Hola mundo!";
 }

Las expresiones lambdas correspondientes son: En VB:

Function() "Hola Mundo!"

En C#

() => "Hola Mundo!";

Veamos un ejemplo concreto muy simple que utilice la expresión lambda anterior. Para eso creamos una aplicación web vacía y le agregamos un Web Form : Primero haremos el caso de Visual Basic:

<%@ Page Language="vb" AutoEventWireup="false" 
   CodeBehind="WebForm1.aspx.vb" 
   Inherits="WebApplication3.WebForm1" %>
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head runat="server">
    <title>Uso de una Expresión Lambda en VB</title>
</head>
<body>
    <form id="form1" runat="server">
    <div>
    <asp:Label ID="Label1" runat="server" ></asp:Label>
    </div>
    </form>
</body>
</html>

Ahora en el archivo "CodeBehind" escribamos lo siguiente:

Public Class WebForm1
    Inherits System.Web.UI.Page
    Protected Sub Page_Load(ByVal sender As Object, 
                            ByVal e As System.EventArgs) 
                                  Handles Me.Load
        Dim miFuncion As Func(Of String) = 
                            Function() "Hola Mundo!, desde VB.Net"
        Label1.Text = miFuncion()
    End Sub
End Class

Ahora en C#

<%@ Page Language="C#" AutoEventWireup="true" 
       CodeBehind="WebForm1.aspx.cs" 
       Inherits="WebApplication2.WebForm1" %>
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head runat="server">
    <title></title>
</head>
<body>
    <form id="form1" runat="server">
    <div>    
        <asp:Label ID="Label1" runat="server" ></asp:Label>
    </div>
    </form>
</body>
</html>

El correspondiente archivo "code behind" en C#:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Web;
using System.Web.UI;
using System.Web.UI.WebControls;

namespace WebApplication2
{
    public partial class WebForm1 : System.Web.UI.Page
    {
        protected void Page_Load(object sender, EventArgs e)
        {
             Func<string> miFuncion = () => "Hola Mundo!, desde C#";
             Label1.Text = miFuncion();
        }
    }
}

En la figura 1. vemos las salidas de ambas páginas:

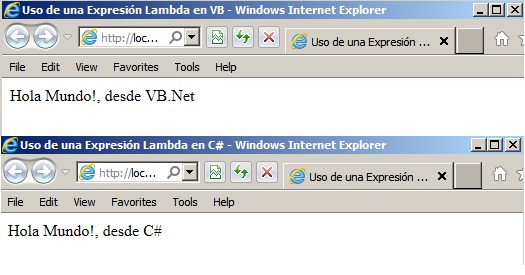Figura 1 - Ambas páginas, escriben el saludo a partir de una expresión lambda definida en el código por detrás.

En C#:

Func<string> miFuncion

En VB:

Dim miFuncion As Func(Of String)

Vemos que en la asignación, le asignamos precisamente la expresión lambda correspondiente:

C#:

 Func miFuncion = () => "Hola Mundo!, desde C#";

VB:

 Dim miFuncion As Func(Of String) = Function() "Hola Mundo!,  " + _
                              "desde VB.Net"